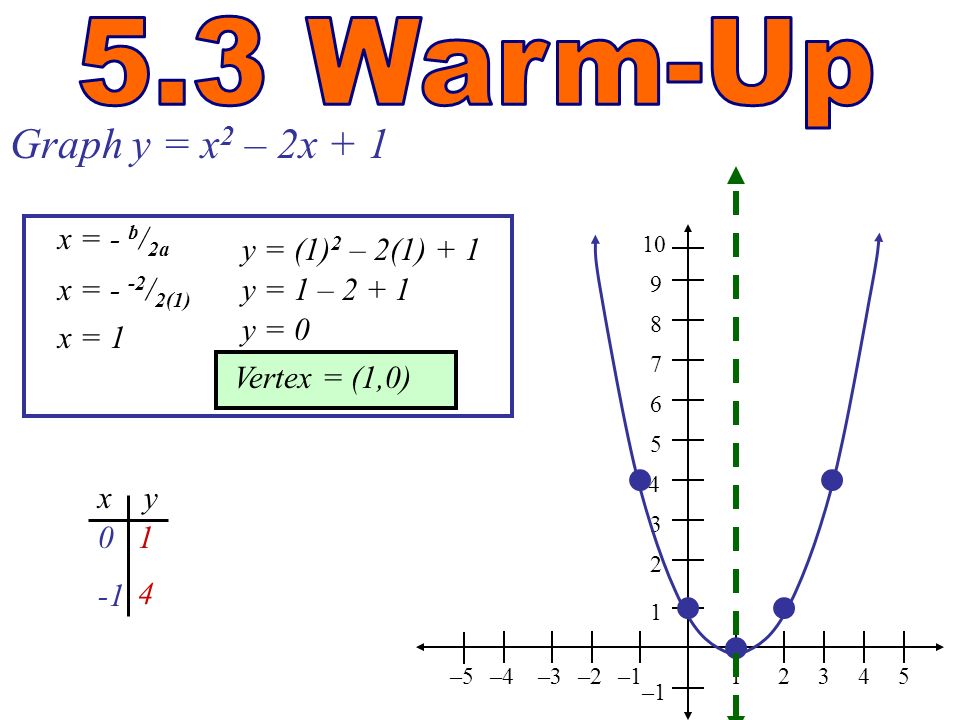
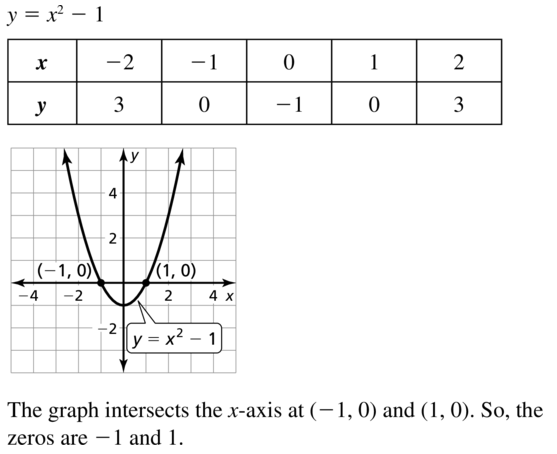
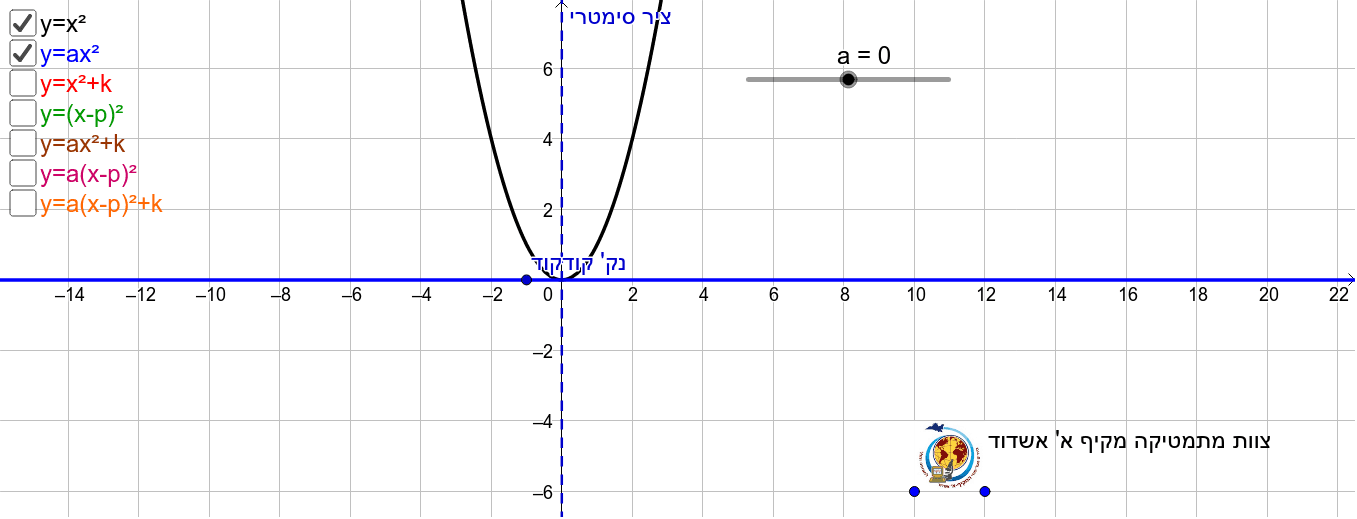
++ 50 ++ parabola y=x^2 1 y=19-(x)^2 152272

Se muestra la ecuacion de una parabola en su forma reducida (x2)^2=8(y4) Se determina vertice, foco y recta directriz de la parabola Se realiza un boceto y = x² b x 3 = (xb/2)² 3 b²/4 Entonces observemos que el vertice sera (b/2, 3b²/4) pero segun el dato es (2,1) entoncesb/2=2 => b=4 Publicidad Publicidad teefiflores96 teefiflores96 Respuesta podras explicar bien el procedimiento o como es la formula?I do not know how to graph the parabola y= x^2Plot a few points and draw a smooth curve thru them If x = 2, y = 4 giving you (2,4) If x = 1, y = 1 giving you (1,1) If x = 0, y = 0 giving you (0,0) If x = 1, y = 1 giving you (1,1) If x = 2, y = 4 giving you (2,4) ===== Cheers, Stan H Answer by jim_thompson5910() (Show Source) You can put this solution on YOUR

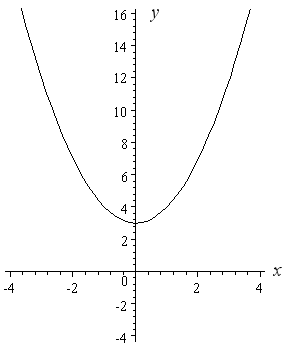
How To Draw Y 2 X 2 Interactive Mathematics

Parabola y=x^2 1 y=19-(x)^2

Parabola y=x^2 1 y=19-(x)^2-Y = (x 3)2 y = (x 3)2 y = x2 3 y = x2 3 Weegy TheClick here👆to get an answer to your question ️ Parabolas y^2 = 4a(x c1) and x^2 = 4a(y c2) , where c1 and c2 are variable, are such that they touch each other Locus of their point of contact is

Chapter 4 Quadratic Functions And Various Nonlinear Topics

Per la tangenza con la retta y = 2x1, basta imporre che il sistema ˆ y = ax2 bxc y = 2x 1 abbia soluzioniAnswer by stanbon(757) (Show Source) You can put this Updated 4/1/18 PM 1 Answer/Comment yumdrea M A term or a sum of terms whose variables have whole number exponents is polynomial Added 4/1/18 PM This answer has been confirmed as correct and helpful Which of the following equations is of a parabola with a vertex at (3, 0)?

V 1 1) = 1 2) 1 16 25 16 2 X 3) = 1 4) =1 25 9 25 A bridge is in the shane of a gomilli ve पर 22 4And then times while then times two x plus zero, which just gives us, um negative 16 over X squared Plus four square Okay, So this is our derivative d y the X And then for a part, a Well, I'm gonna find the equation of the tangent line to the graph at the 02 where we find the slope of the tangent line at X is equal to zero So theParabola 3 3) 5x² – 3y2 = 32 4) 3x² 5y Axes are coordinate axes, S and S' are foci, B and B1 are the ends of minor axis, 4 1 SBS' = sin 5 JArea of SBS'B' is sq units, then the equation of the ellipse is 2 2 2 12 y ?

The mirror image of the parabola y^(2)=4x in the tangent to the parabola at the point (1,2) is (a)(x Vertex of parabola is (2 , 1) equation of directrix x y 1 = 0 we know, directrix is perpendicular upon axis of parabola so, Let equation of axis of parabola is x y k = 0 we know, product of slopes of perpendicular line is 1 we also know, vertex lies on axis of line so, (2 , 1) lies on x y k =0 so, 2 1 k = 0 k = 3Graph a parabola by finding the vertex and using the line of symmetry and the yintercept

2

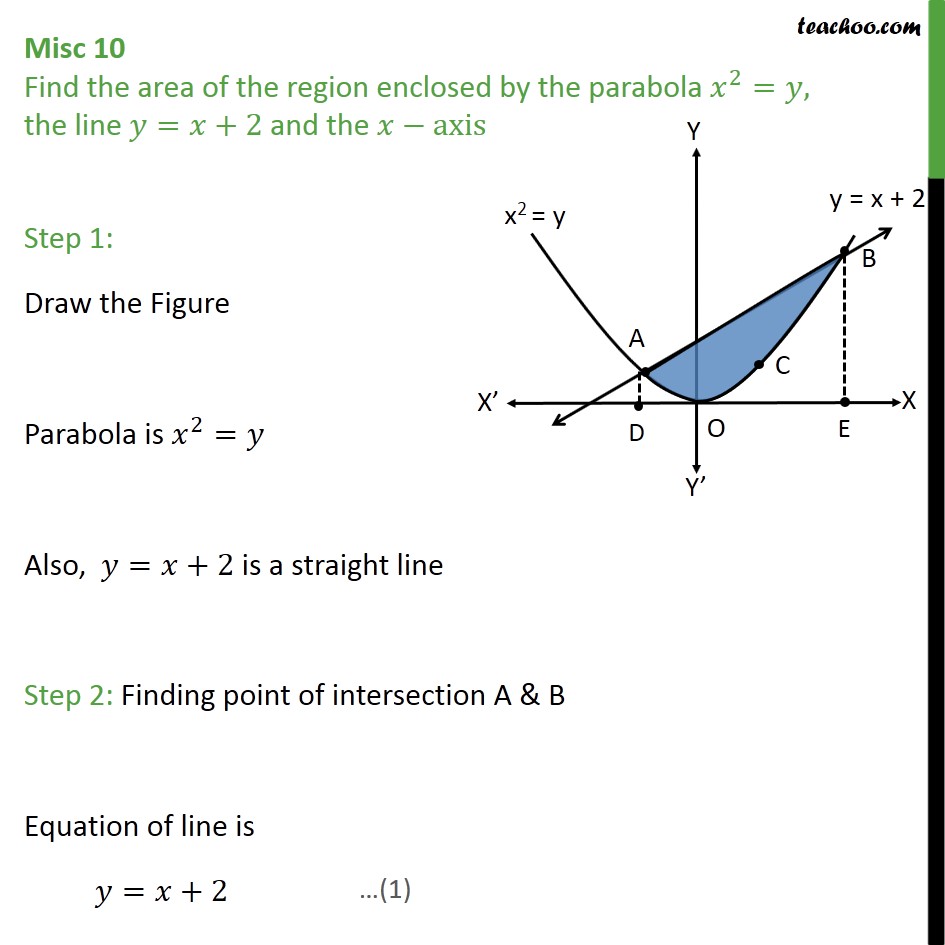
Misc 10 Find Area Enclosed By Parabola X2 Y T X 2

Graph the parabola y=(x3)^21 Mathematics Answer Comment 1 answer trapecia 35 3 months ago 4 0 Answer Stepbystep explanation y = (x3)²1 This is the equation for an upopening parabola with vertex (3,1) Find the xintercepts 0 = (x3)²1 (x3)² = 1 x3 = ±1 x = 4, 2 The graph crosses the xaxis at (4,0) and (2,0) Find the yintercept y = (03)²1 = 8 The3 What are the foci of the ellipse with equation x24y2=36?Kakarot_15 0 users composing answers 2 0 Answers #1 1 y=−1/12x^2−2x−1 factor as y = (1/12) x^2 24x 12 complete the square on x y = ( 1/12) x^2 24x 144 12 144 y = (1/12) ( x 12)^2 132 y = (1/12) (x 12)^2 11 (y

Graphing Quadratic Functions

Graphing Quadratic Functions

Were given equation by physical to minus off three X minus one Bowl square plus two, Will you?By signing up, you'll get thousands of stepbystep solutions to your homeworkThe equation of the common tangents to the parabola y = x2 and y = (x 2)2 is / are (a) y = 4(x1) (b (c) y = 4(x1) (d) y = 30x50

Quadratic Functions

14 2 Limits And Continuity

Gracias Explicación paso a paso Publicidad Publicidad Nuevas preguntas de Matemáticas (5m3)² Por The equation of a parabola is given y=−1/4x^24x−19 What are the coordinates of the vertex of the parabola?1What is the equation of the directrix of the parabola with equation x=4y216y19?

Math Scene Equations Iii Lesson 3 Quadratic Equations

How To Find The Equation Of A Parabola Given Its Zeros And A Point Quora

Parabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose theUse the distributive property to multiply y by x 2 1 Add x to both sides Add x to both sides All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, Solo llevas a la ecuación a la forma genérica de la ecuación de una parábola y= 2x^2x2y= 2(x^2x/21) , saco factor común 2y= 2(x^2x/21 1/16 1/16) , Hola0002 Hola0002 Matemáticas Bachillerato contestada El vertice de la parábola que corresponde a la función y=2x^2x2 es A (1/4, 19/8) B (1/4, 19/8) C (1/4, 15/8) D (1/4, 15/8) ¿Cual es la

Chapter 4 Quadratic Functions And Various Nonlinear Topics

Graphing Quadratic Functions

Determinare l'equazione della retta t tangente alla parabola y = x 2 2x 1 e parallela alla retta 4x y 4 = 0 Si scrive l'equazione 4x y k = 0 del fascio improprio di rette parallele a 4x y 4 = 0 Si mettono a sistema l'equazione della parabola e l'equazione del fascio e si impone la condizione di tangenza ∆ = 0 Si ottiene 8 – k = 0 da cu i k = 8 Sostituendo tale valore A x 2 B x y C y 2 D x E y F = 0 or equivalently, we can write it as ( x y 1) ( A B / 2 D / 2 B / 2 C E / 2 D / 2 E / 2 F) ( x y 1) = 0 (we will denote the above 3x3 matrix with M) So, let's say you are given a conic section v τ M v = 0 and let's say we want to rotate it by angle φ Look at the explanation section Given y=1/2x^2 Since it has no constant term, Its vertex and intercept is (0,0) Take a few points on either side of x=0 Find the corresponding y value Tabulate the va;ues Plot the pair of points Join all the points You get the parabola

Curve Fitting And Solution Of Equation

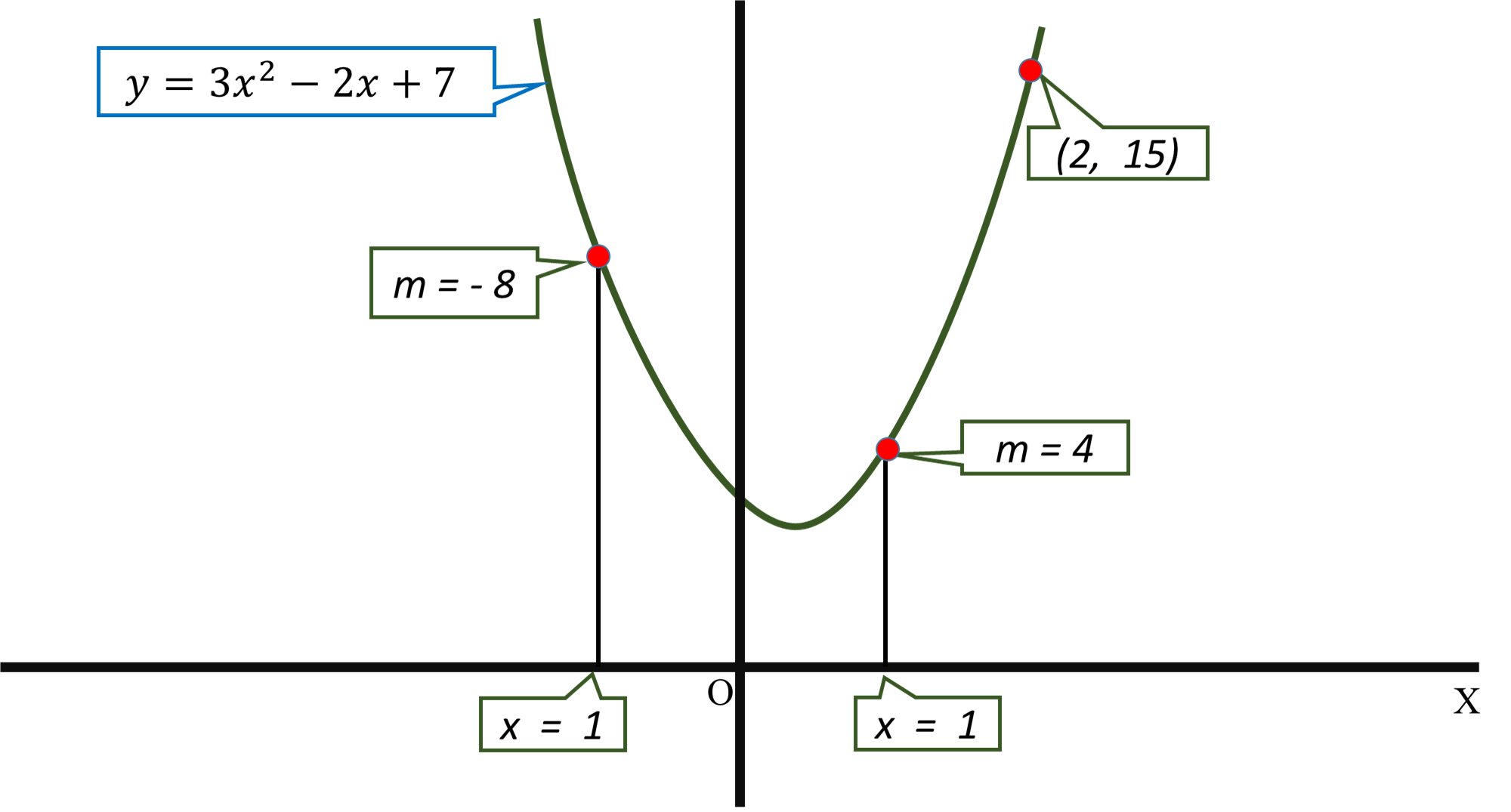
How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic

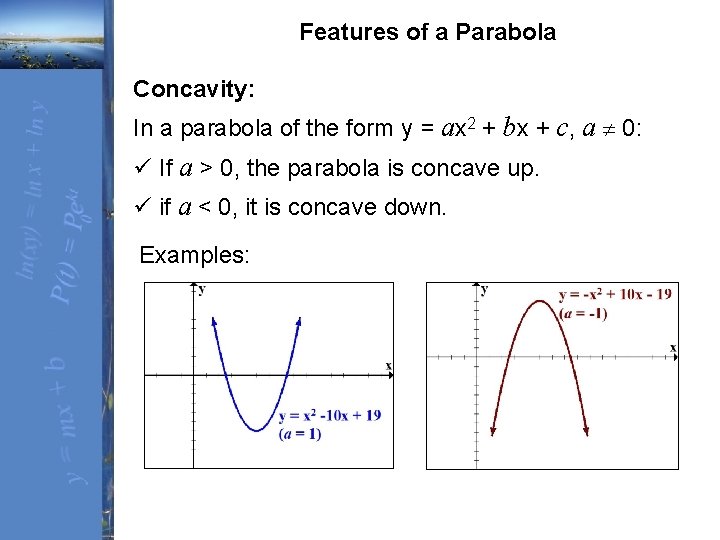
Calculadora gratuita de parábolas Calcular os focos, vértices, eixos e diretriz de uma parábola passo a passoLa parabola ha quindi equazione y = x2 −x−1 Esercizio 12 Determinare le equazioni delle parabole con asse parallelo all'asse delle y, tangenti alla retta y = 2x 1 e passanti per i punti A(0,2) e B(−1,3) Soluzione La parabola ha equazione del tipo y = ax2 bxc;Key Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;

Graphing Quadratic Functions

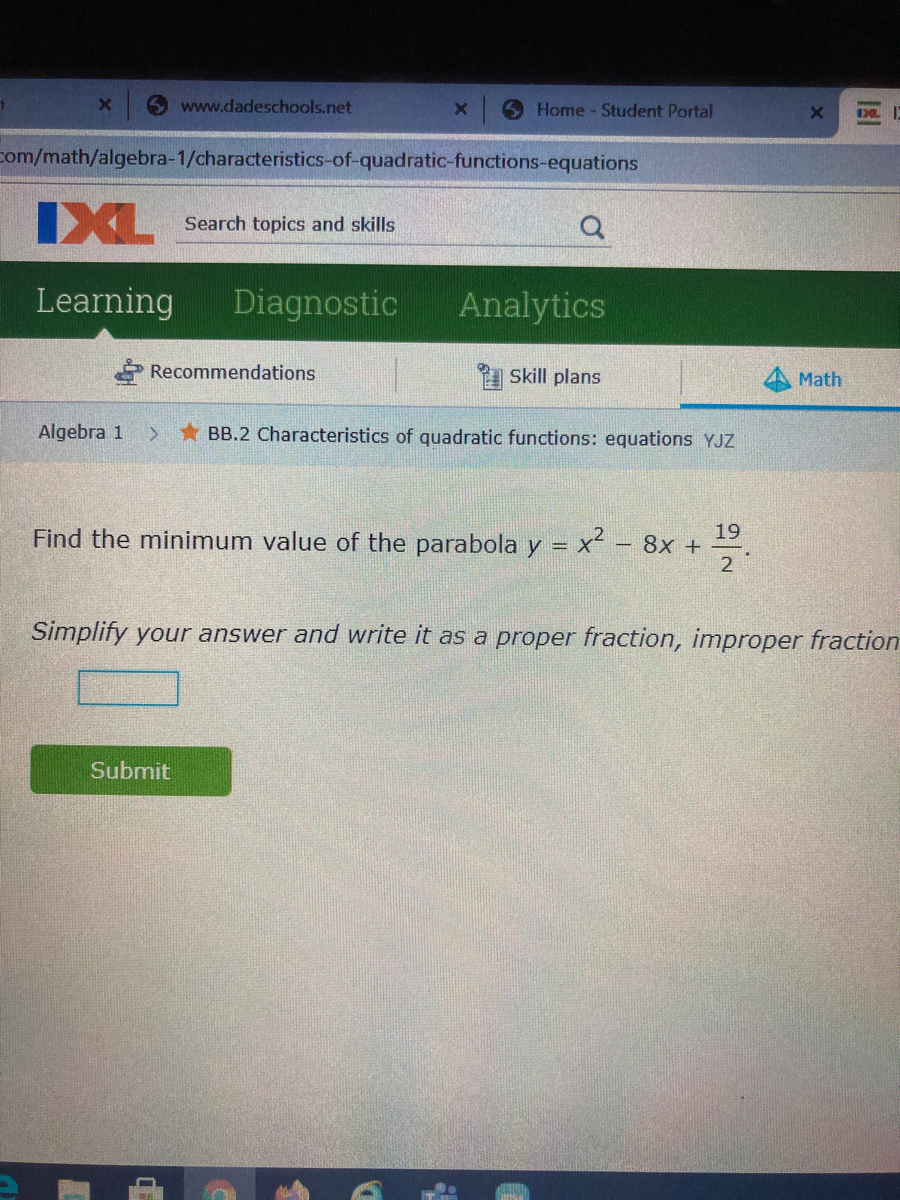
Answered 19 Find The Minimum Value Of The Bartleby

When graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if a1 See answer Alphie24 is waiting for your help Add your answer and earn points harpazo harpazo y = −1/4x^2 4x − 19 1 Use x = b/2a to find x x = 4/2(1/4) x = 4/(1/2) x = 4/1 • (2/1) x = 8/1 x = 8 2 Plug x into the function to find your vertex Replace every xAnswer (1 of 4) Arrange the equation in the vertex form, Y = a(X h)^2 k or general form Y=aX^2bXc The equation is already written in general form Find the vertex by formula for X coordinate X = b/2a and then plugging the value of X in the equation, find Y

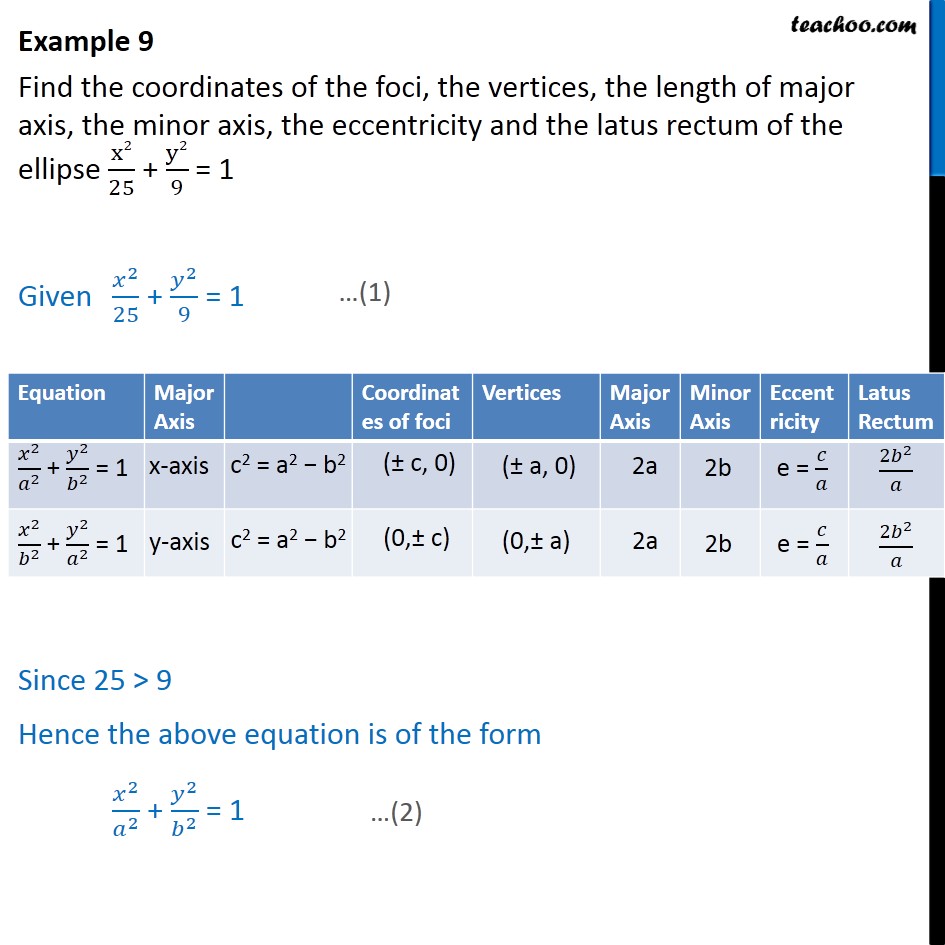
Example 9 X2 25 Y2 9 1 Find Foci Vertices Eccentricity

Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help

X^ {2}8xy1=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x=\frac {8±\sqrt {8^ {2}4\left (y1\right)}} {2}Answer (1 of 7) Yes, its axis of symmetry is the xaxis If you have a quadratic equation in two unknowns, Ax^2BxyCy^2DxEyF=0 you can tell if the curve it represents is a parabola or not by its discriminant B^24AC If the discriminant is 0, it's a parabola;Answer to What is the focus of the parabola y = 14x^2 ?

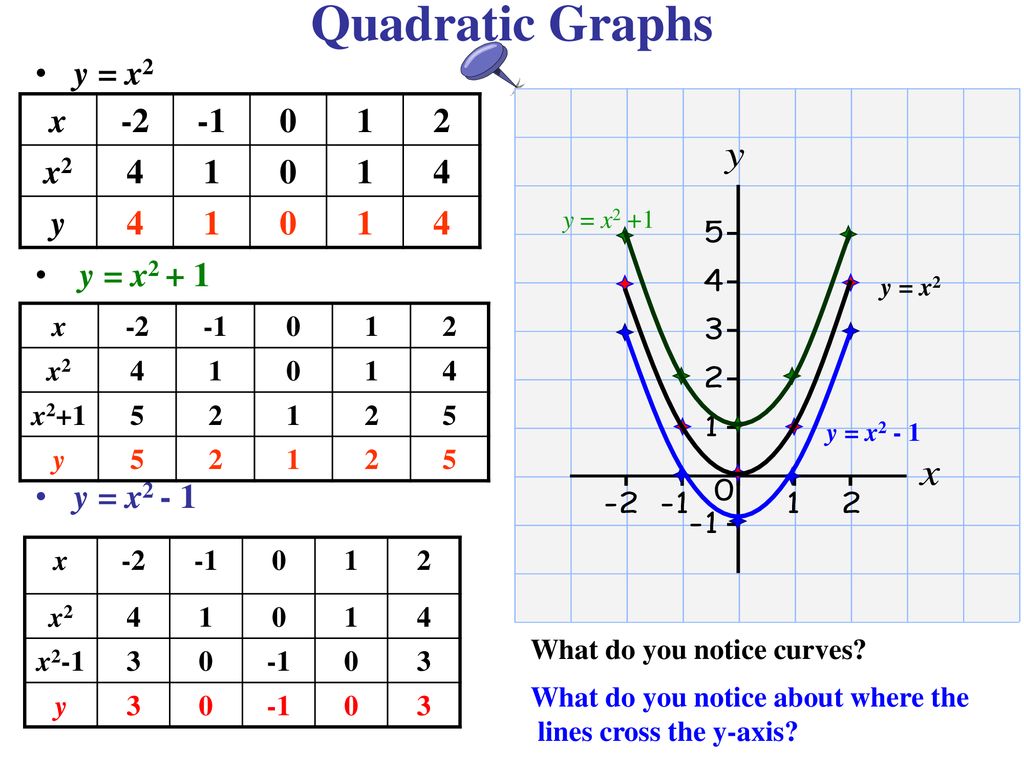
Quadratic Graphs Parabolas Ppt Download

Quadratic Function

 How Do You Graph The Parabola Y 1 2 X 2 Using Vertex Intercepts And Additional Points The focus of a parabola can be found by adding to the y coordinate if the parabola opens up or down substitute the known values of , , and into the formula and simplify find the axis of symmetry by finding the line that passes through the vertex and the focus2 What is the length of the major axis of the ellipse with equation 4(x4)29(y1)236?Autograph is a question So let us solve this equation a bit It is equal to minus three into X square plus one minus two X plus two It is equal to minus three x squared minus tree plus six six plus two is equal to minus three X squared plus six X minus one

Solved Heck Your Answer 21 Y X 10x 16 Practice And Chegg Com

2

Parabola Opens Right Standard equation of a parabola that opens right and symmetric about xaxis with vertex at origin y 2 = 4ax Standard equation of a parabola that opens up and symmetric about xaxis with at vertex (h, k) (y k) 2 = 4a(x h) Graph of y 2 = 4axIt is shown elsewhere in this article that the equation of the parabola is 4fy = x 2, where f is the focal length At the positive x end of the chord, x = c / 2 and y = d Since this point is on the parabola, these coordinates must satisfy the equation above Therefore, by substitution, = () From this, = Area enclosed between a parabola and a chord Parabola (magenta) and line (lower light4 What are the slpoes of the asymptotes of the hyperbola with equation 4x2y28x6y=9?

Systems Of Equations Mathtec

10 The Equation Y 2 8 Y X 19 0 Represents N A A Parabola Whose Focus Is Left Frac 1

Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceCorrect answer to the question In the parabola y = (x 1)2 2, what is the vertex?1 Parabola y=x^28x12 Parabola y=x^28x12Click here👆to get an answer to your question ️ The area (in sq units) bounded by the parabola y = x^2 1 , the tangent at the point (2, 3) to it and the y axis isWhat is the maximum vertical distance between the line y = x 2 and the parabola y = x 2 for −1 ≤ x ≤ 2?

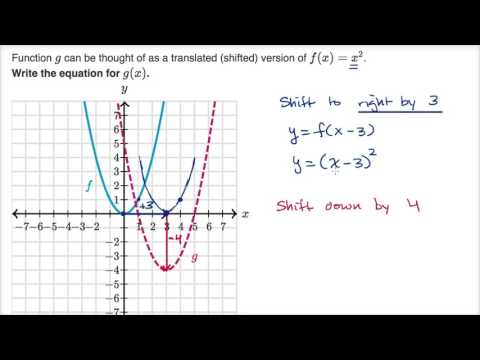
Shifting Parabolas Video Khan Academy

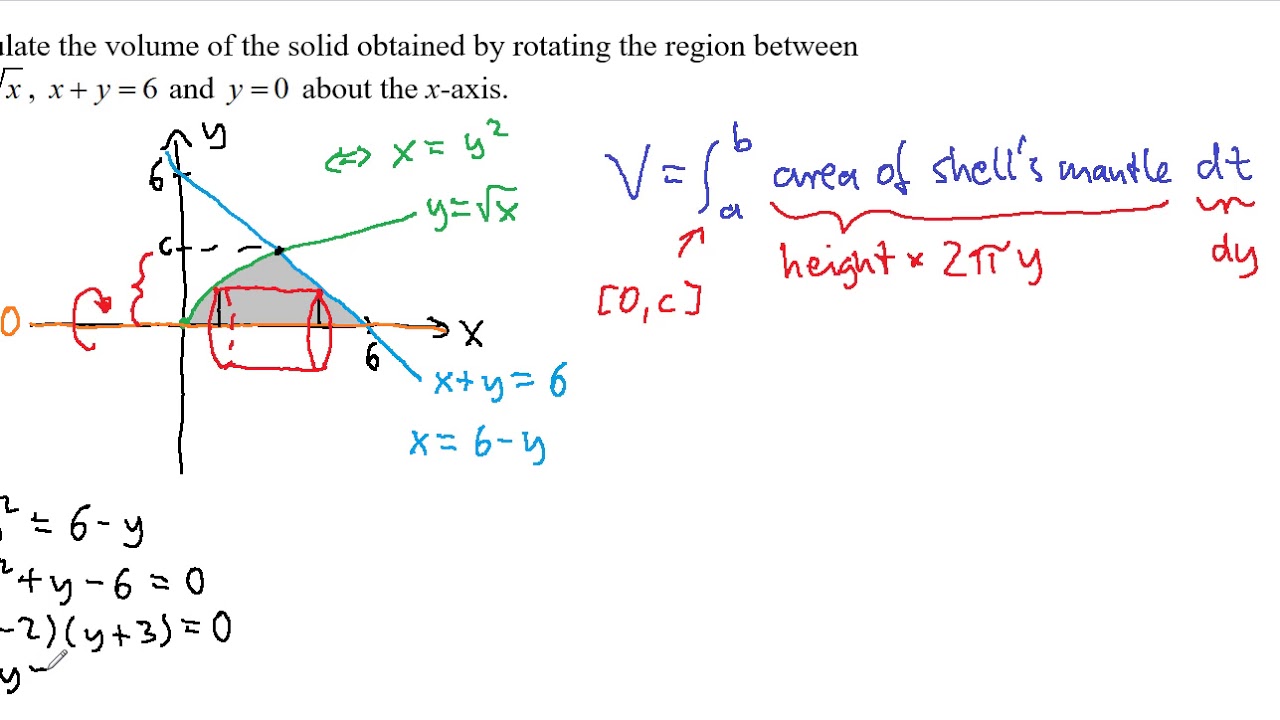
Volume Of Revolution Shell Method

Igualar y y al nuevo lado derecho Use la forma de vértice, y = a ( x − h) 2 k y = a ( x h) 2 k para determinar los valores de a a, h h, y k k Dado que el valor de a a es positivo, la parábola se abre hacia arriba Encuentra el vértice ( h, k) ( h, k) Hallar p p, la distancia desde el vértice al foco Example 7 (y 1) 2 = x If we think about the equation (y 1) 2 = x for a while, we can see that x will be positive for all values of y (since any value squared will be positive) except y = −1 (at which point x = 0) In the equation (y 1) 2 = x, the "plus 1" in brackets has the effect of moving our rotated parabola down one unit ExampleFind the extremities of latus rectum of the parabola y=(x^2)2x3 Ans is (1/2,9/4) (3/2,9/4) i just need full solution i tried it as follo y=x^22x3 x^22x=y3 x^22x1=y31 (x1)^2=1(y2) let X=x1 and Y=y2 then equation becomes X^2=Y on comparing it with x^2=4ay which is general form of parabolic equations we get a=1/4 so according to me extremities of latus rectum should be (0,1

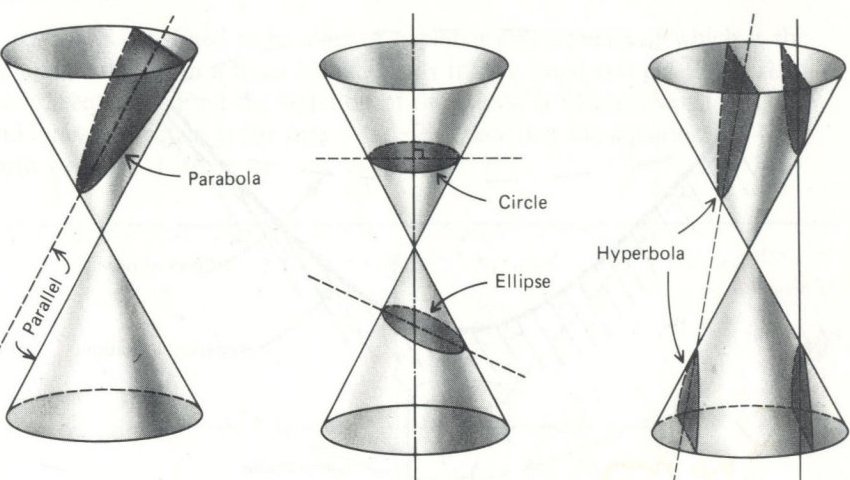
Numbers Quadratic Relations Conic Sections

How To Find Quadratic Line Of Symmetry

 This and congruence of the two parabola imply that `MT` is vertical and `FT=MT` and must line one directrix of `y=x^(2)x1` So, `y=3/4` The tangent line at `T` makes equal angle with `FT` and with as vertical lineClick here👆to get an answer to your question ️ The area of the region bounded by the parabola (y 2)^2 = x 1 , the tangent to the parabola at the point (2, 3) and the x axis is?Consider two parabola `y=x^2x1 and y=x^2x1/2,` the parabola `y=x^2x1/2` is fixed and parabola `y = x^2 1` rolls without slipping around the fixed par Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra

1 Point Consider The Line L T 2 3t 6 T Then L Intersects 1 The X Axis Homeworklib

Answered 13 Graphing Shifted Parabolas An Bartleby

Graph y=1/4x^2 y = 1 4 x2 y = 1 4 x 2 Combine 1 4 1 4 and x2 x 2 y = x2 4 y = x 2 4 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 4 x 2 4 First, let's divide both sides by 8 to get x = (y2)^2/8 (y 2)^2 >= 0 for all values of y, but will equal 0 when y = 2 So the parabola has its vertex to the left on the y axis at (0, 2) and its axis is a horizontal line parallel to the x axis with formula y = 2 It is symmetric about this axis The means that for every point (x, y) that lies on the parabola, so does the point (x, (4y))Free Hyperbola calculator Calculate Hyperbola center, axis, foci, vertices, eccentricity and asymptotes stepbystep

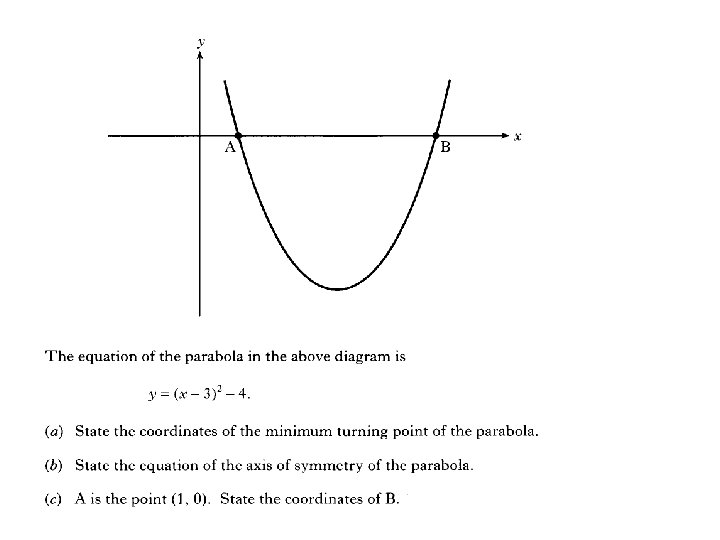
Quadratic Function 2 Www Mathsrevision Com Nat 5

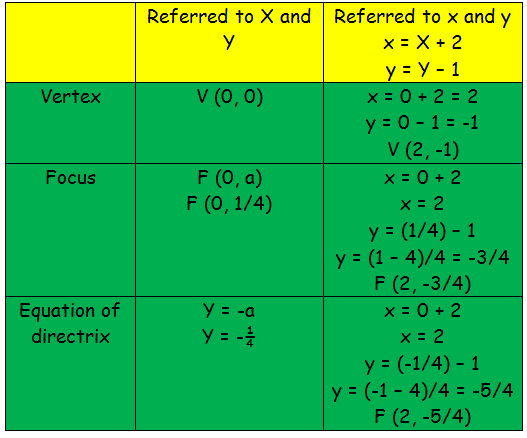
How To Find Focus Directrix And Vertex Of Parabola

 The area (in sq units) bounded by the parabola y = x^2 1, the tangent at the point (2, 3) to it and the yaxis asked in Mathematics by Simrank (721k points) jee mains 19 1 vote 1 answer Let a, b and λ be positive real numbers Suppose P is an end point of the latus rectum of the parabola y^2 = 4λx, asked in Mathematics by Anjali01 (476kThe vertex of the parabola (y2)^(2) = 16(x1) is Apne doubts clear karein ab Whatsapp par bhi Try it now CLICK HERE 1x 15x 2x Loading DoubtNut Solution for you Watch 1000 concepts & tricky questions explained! The equation of a parabola is given y=−1/12x^2−2x−1 What are the coordinates of the focus of the parabola?

Quadratic Functions

Ch 5 Notes Ppt Video Online Download

If positive, a hyper97 K views 400 people like this Like Share Share Answer Text `(1,2)`(2,1)(1,2)`(1,2)` Related Video

The Particle Travels Along The Path Defined By The Parabola Y 0 5x 2 If The Component Of Velocity Along The X Axis Is Vx 5t Ft S Where T Is In Seconds Determine The Particle S Distance

Ex 6 3 15 Find Equation Of Tangent Line To Y X2 2x 7

2

Assignment Previewer

Graphing Parabolas

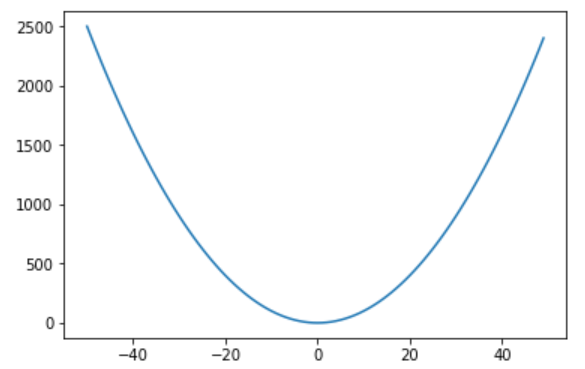
Python Program To Plot The Function Y X 2 Using The Pyplot Or Matplotlib Libraries By Karthika A Guvi Medium

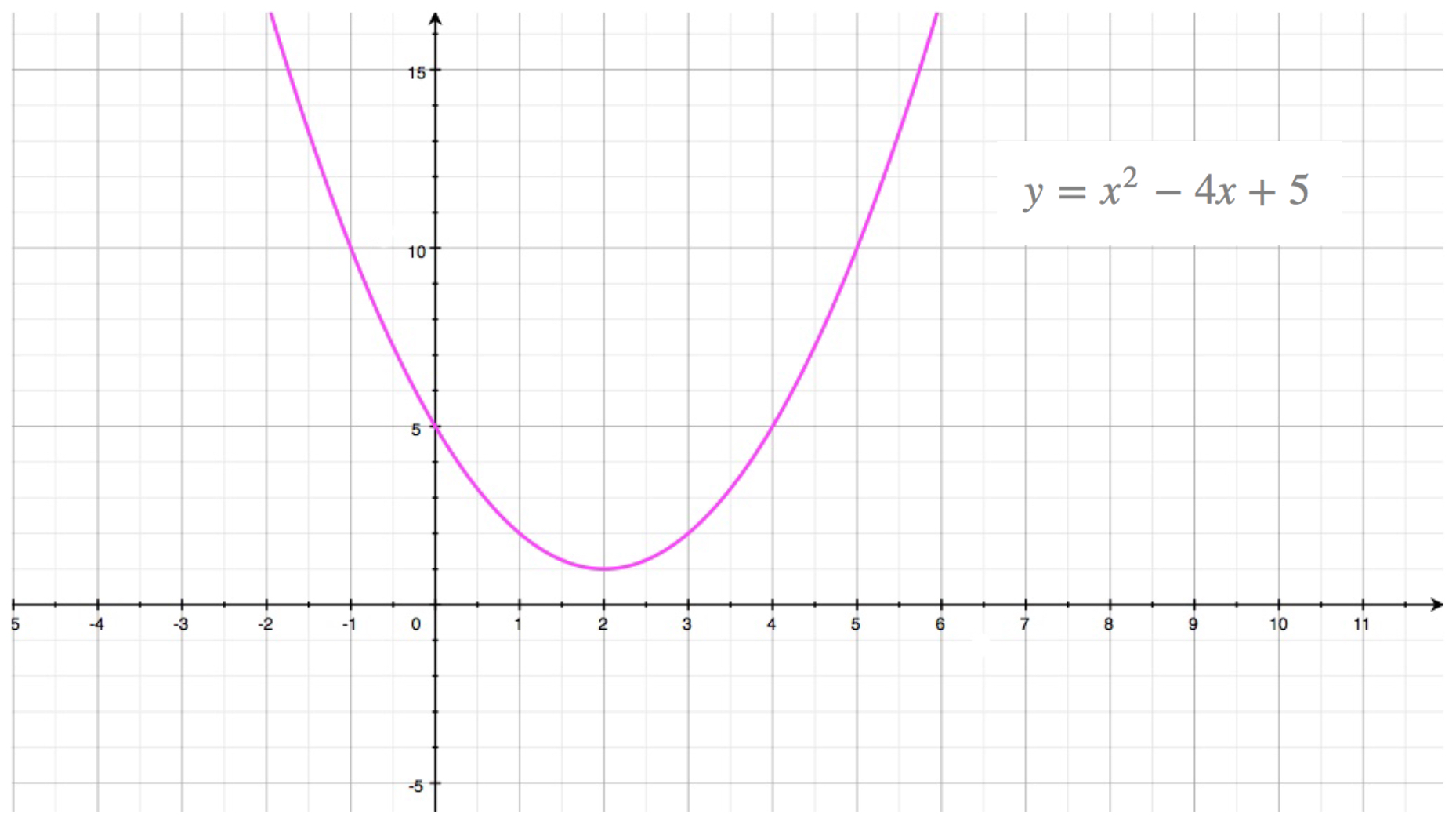
Quadratic Function Parabola

Graphing Quadratic Functions Ppt Download

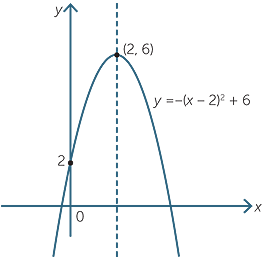
Quadratic Function

2

1

Parabolas

2

Objective 19 Finding A Quadratic Model Knowing The Vertex And

Example 8 Find Equation Of Parabola Symmetric About Y Axis

Big Ideas Math Algebra 1 Answers Chapter 8 Graphing Quadratic Functions Ccss Math Answers

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

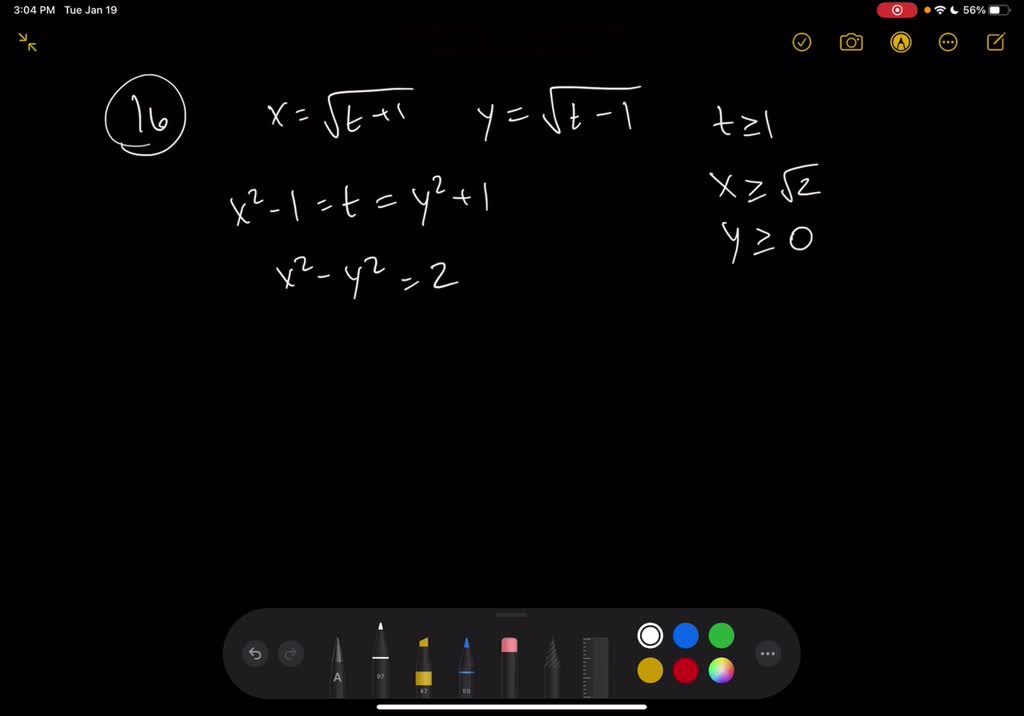
Solved Find A Parametrization Of The Curve That Is A Portion Of The Parabola Y X 2 That A Joins The Origin To The Point 2 4 I B Joins The Point 1 I To The Origin

Graphing Quadratic Functions

Quadratic Functions

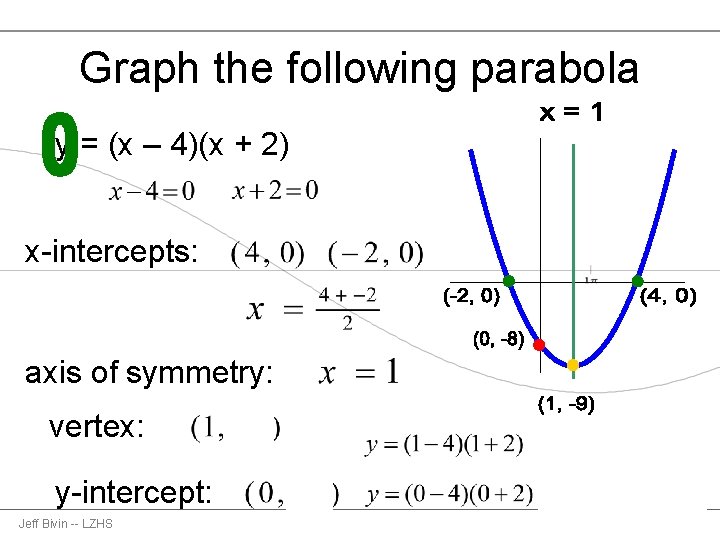
Graphing Parabolas Using The Vertex Axis Of Symmetry

What Is The Vertex Of Y X 2 4x 1 Socratic

This Professor S Amazing Trick Makes Quadratic Equations Easier The New York Times

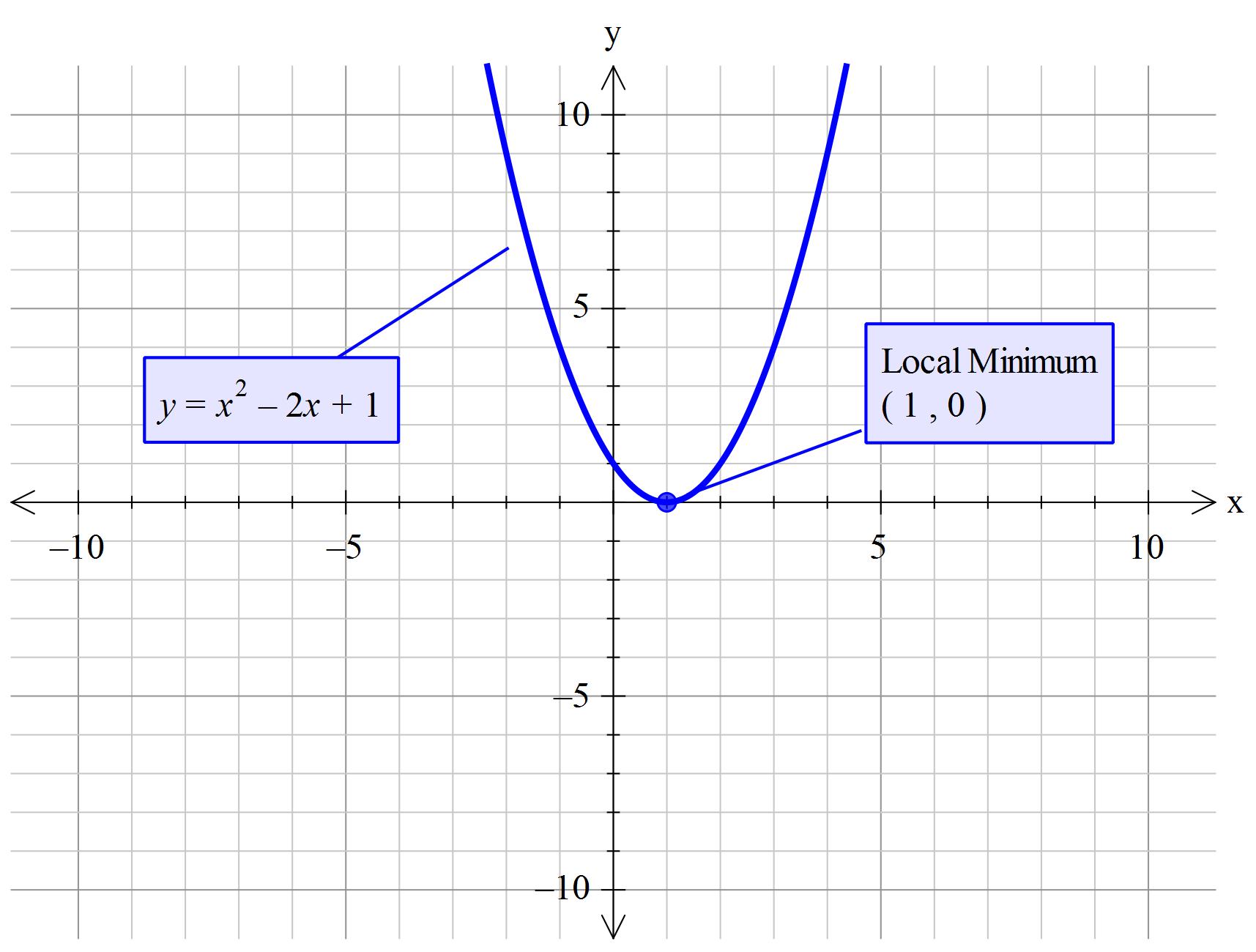
What Is The Vertex Of Y X 2 2x 1 Socratic

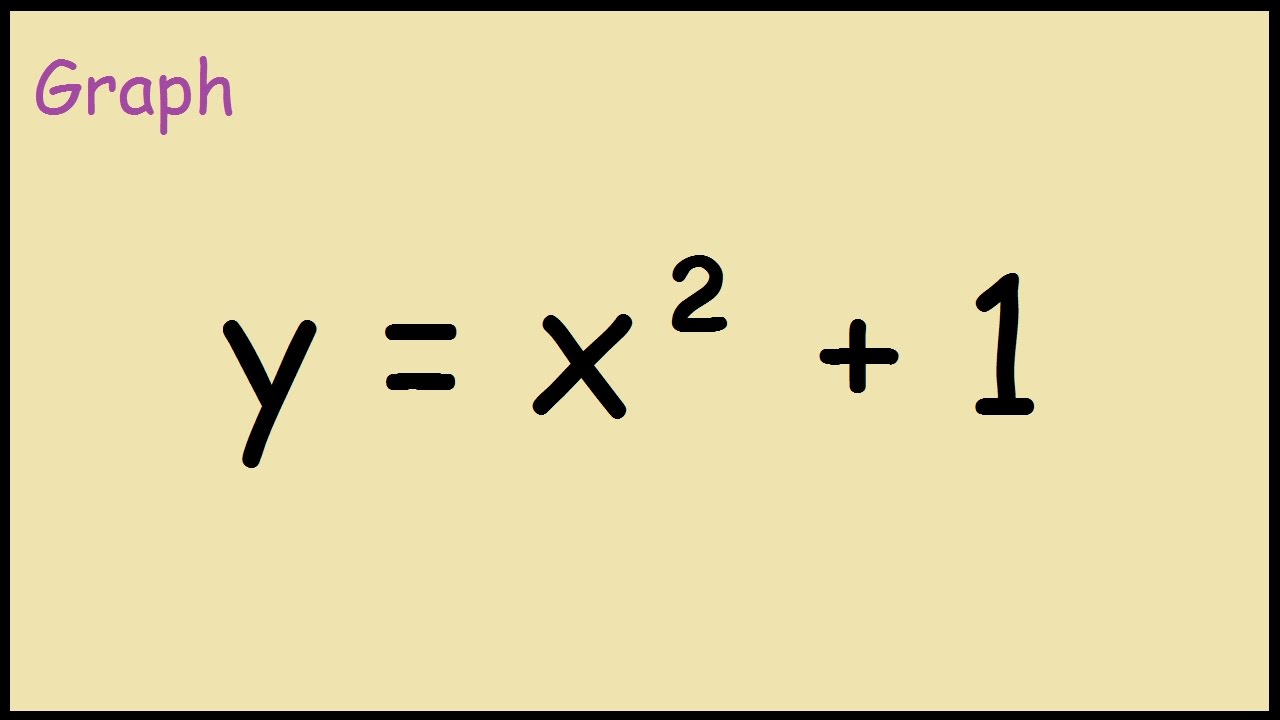
How To Graph Y X 2 1 Youtube

Solved 9 10 X 1 2 Y 1 2 36 64 11 4x2 25y2 50y Chegg Com

Let R Be The Region Between The Parabolas Y X 2 8x 4 Space And Space Y 6 X 2 Express As An Integral The Volume Of The Solid

Let P Be The Point On The Parabola Y 2 4x Which Is At The Shortest Distance From The Center S Of The Circle X 2 Y 2 4x 16y

Illustrative Mathematics Algebra 2 Unit 3 19 Teachers Im Demo

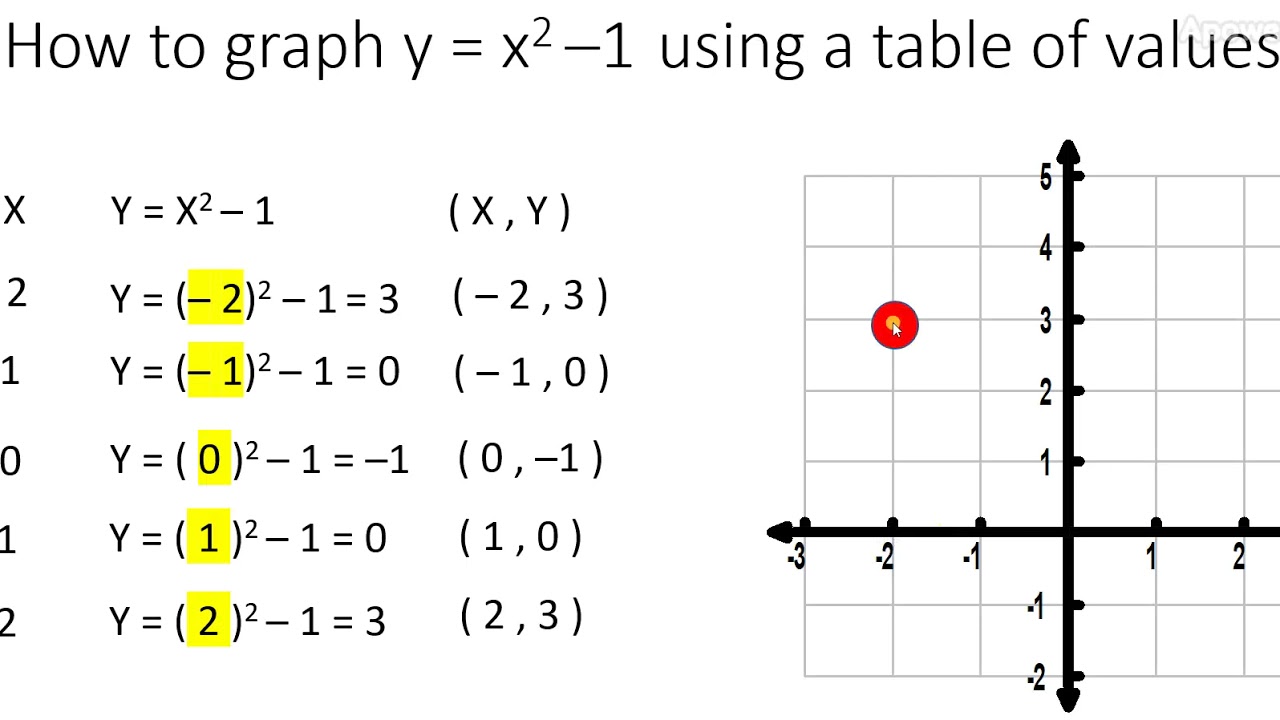
Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube

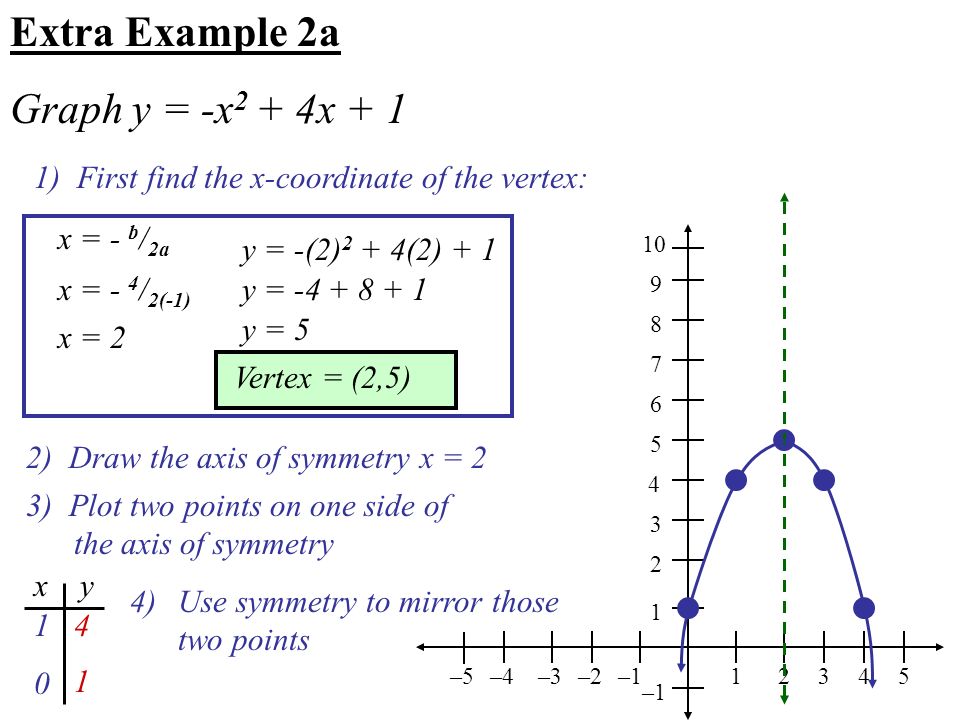
Ch 5 Notes Ppt Video Online Download

Conic Section Wikipedia

2

Solved Find The Equation Of The Parabola With Its Focus At 7 6 And Its Directrix At Y 4 Question 17 Options A Y 4 X 5 7 B Y 4 X 7 Course Hero

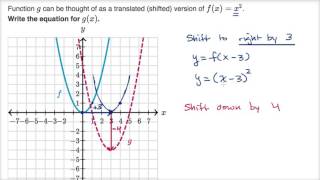
Shifting Parabolas Video Khan Academy

Y X 2 6x 12 Graphed And Shade The Side That Needs To Be Shaded Mathskey Com

Parabola Complete

Quadratic Function

Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help

Solved Graph Each Parabola And Give Its Vertex Axis Of Chegg Com

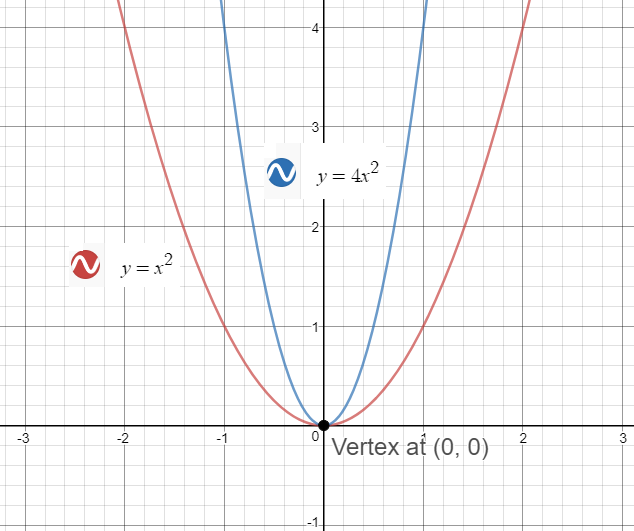
How To Graph A Parabola Y 4x 2 Socratic

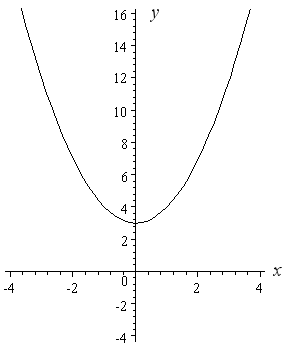
How To Draw Y 2 X 2 Interactive Mathematics

2

Parabola Y X 2 Geogebra

Shifting Parabolas Video Khan Academy

Solved 7 1 Ws Graph Each Parabola Identify The Vertex Chegg Com

How Do You Graph The Parabola Y 2 X 1 2 5 Using Vertex Intercepts And Additional Points Socratic

1

2

2

Consider The Function F X 2 X 2 Ppt Video Online Download

How To Draw The Parabola With Equation X Y 2 2 Tex Latex Stack Exchange

1

Quadratic Function

Dan It Turns Out That The Idea Of How Fast Does A Function Grow At Each Point Can Also Be Expressed As A Function That S Called An Original Function S Derivative

Solution For Quadratic Functions Sketch Two Parabolas Showing All Procedure Concavity Y Intercept X Intercept Symmetric Axis And Vertex Point A Y 2x 2 3x 1 B Y 3x 2 2x 1

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Tinkutara Equation Editor Math Forum Question

Ap Calculus Ab Worksheet 19 Tangent And Normal Lines Power Rule I Only Need Help On 9 13 And 14 Please Homeworkhelp

6 6 Analyzing Graphs Of Quadratic Functions

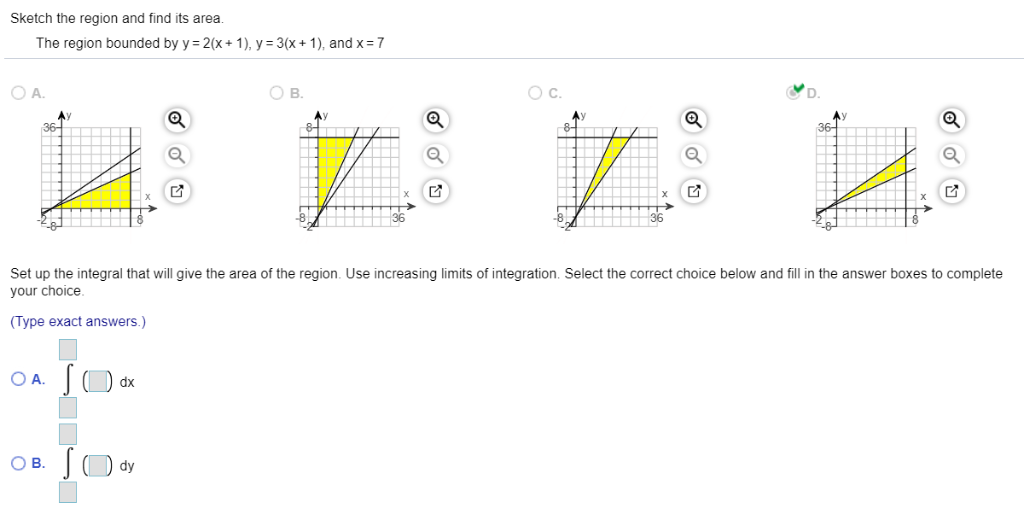
Solved In The Figure To The Right The Equation Of The Solid Chegg Com

How To Find And Graph The Vertex Axis Of Symmetry Focus Directrix And Direction Of Opening Of The Parabola Given These Equations I 4 Y 2 X 4 2 Ii Y 8 2 4 X 4 And Iii Y 1x 2 2 3x 19 2

1

Graphing Parabolas

2

Core Connections Algebra 2

The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com

Solution Can You Please Help With The Following Question For The Parabola X 2 8x Y 19 0 1 Convert The Equation To Vertex Form 2 Find The Vertex 3 Find The Axis Of Symmetr

Graphing Parabolas

Solved A Rectangle Is Constructed With Its Base On The X Axis And Two Of Its Vertices On The Parabola Y 361 X What Are The Dimensions Of The Course Hero

2

2